LAVORO
DELLA FORZA GRAVITAZIONALE
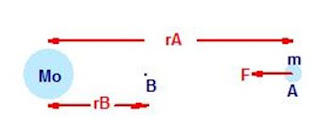
F = G*Mo*m
/ rA² .
Vogliamo dimostrare che il lavoro di questa
forza nello spostare la massa ' m '
dalla distanza ' rA ' alla ' rB ' è
dato da :
L(AB)
= G * Mo *
m * (1 / rB - 1 / rA).
Dato che l'intensità della forza, durante
lo spostamento non è costante (va aumentando), im-
maginiamo di dividere lo spostamento (rA
- rB) in un numero grandissimo di parti, teorica-
mente infinito, in modo che in ognuna, la
forza possa essere considerata costante.
Basterà calcolare il lavoro nel primo
spostamento dalla distanza rA alla distanza
r1 (del
primo punto, vicinissimo ad A e
alla sua sinistra), per riuscire a calcolare tutti gli altri .
Risulta infatti : L(A1) = G * Mo
* M * (rA - r1) / r1*rA. Da
notare che al posto di
r2 abbiamo
messo il prodotto r1*rA,
dato che le due distanze sono quasi uguali.
(Sarebbe come dire che al
posto di 4 mettiamo il prodotto : 2 *
2,000000001).
Se dividiamo ciascuna distanza (all'interno
della parentesi) per r1*rA , avremo :
L (A1)
= G * Mo * m * (1 / r1 - 1 / rA)
Questa formula ci insegna a calcolare tutti
gli altri termini, anche se in numero ... infinito.
L(12)
= G * Mo * m * (1 / r2 - 1 / r1)
L
(23) = G * Mo * m * (1 / r3
- 1 / r2)
.......................................................
L (xB)
=
G * Mo * m * (1 / rB
- 1 / rX)
Per ottenere il valore L(AB)
cercato, basterà sommarli tutti. Se mettiamo in evidenza il fattore comune
(G*Mo*m) nella somma si elidono tutti i termini, tranne - 1 / rA ed 1 /
rB, per cui risulta
(1)
L
(AB) = G * Mo * m * (1 / rB
- 1 / rA) ( .... come se A e B fossero
vicinissimi )
Il lavoro sarà positivo (quindi
fatto dal campo) se m viene avvicinata ad Mo e negativo (spesa di
energia) per allontanare
m da Mo.
00000000000000000000000000000000
(1)
L (AB)
= G * Mo * m * (1 / rB - 1 / rA)
Questa importantissima formula ci
consentirà di studiare problemi nei casi di spostamenti di una massa in grandi
distanze e sulla Terra quando appunto le distanze sono tali che il peso non può
essere considerato costante.
Un lavoro negativo in pratica vuol dire che
il campo gravitazionale non può allontanare i corpi, ma solo avvicinarli. Il
lavoro del campo gravitazionale se le
due masse vengono allontanate è negativo e
si deve infatti spendere energia per ottenerlo.
Per distanze dalla superficie della Terra
di circa 2000 metri il peso di un corpo è considerato costante e come livello
di energia potenziale zero si prende solitamente il suolo o il livello più
basso.
Nel caso che si debba usare la (1) vediamo
che se rB tende all’infinito dato che 1/rB tende a zero
la (1) diventa un monomio che ci fornisce il lavoro necessario per allontanare
m dalla distanza iniziale rA all’infinito e prendiamo questo valore
come energia potenziale nel punto A a distanza rA dal centro del
pianeta.
L’energia potenziale gravitazionale UA
= - G*Mo*m / rA ad altezze maggiori è maggiore (meno negativa) e il campo tende
sempre ad avvicinare le masse quindi da punti di energia potenziale maggiori
verso punti a energie potenziali minori.
Siamo
in grado di calcolare la velocità di fuga dalla superficie
terrestre di un grave.
La sua velocità iniziale Vf deve
avere un valore tale che (pur diminuendo continuamente nella salita) si annulli
a distanza infinita dove l’energia potenziale è anch’essa nulla.
Quindi : - G*Mo*m /
R(terrestre) + m*Vf 2 /
2 =
0.
Quindi la velocità di fuga (per qualsiasi
massa) vale :
Vf =
= 11.2
(km/s)
ooooooo
ooooooo


Nessun commento:
Posta un commento