Una
sferetta di data massa m1 viene lanciata
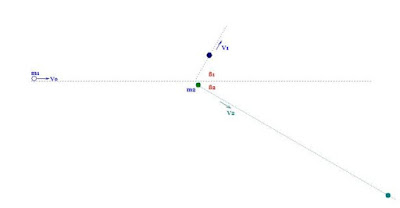
con una velocità Vo contro una seconda sferetta di massa m2, inizialmente ferma.
Se si conoscono i
valori di Vo, delle due masse (m1 ed m2), il valore di V1 e dell'angolo ß1
,
verranno calcolate V2
e ß2 .
Inoltre verrà fatto un bilancio energetico e
si capirà se si tratta di urto elastico o anelastico.
Dato che la quantità di moto è una
grandezza vettoriale, considereremo la conservazione del-
le sue componenti sui due assi. La quantità
di moto iniziale, lungo l'asse x,
vale m1*Vo , men-
tre quella finale vale : m1*V1*cos
( ß1 ) + m2*V2*cos ( ß2 ) , quindi scriveremo :
(1) m1*Vo = m1*V1*cos ( ß1 ) + m2*V2*cos
( ß2 )
La quantità di moto iniziale, lungo l'asse y , è nulla e
tale dovrà rimanere, quindi scriveremo :
(2) 0
= m1*V1*sin
( ß1 ) - m2*V2*sin ( ß 2
)
Risolvendo il sistema di queste due equazioni potremo
ricavare le due incognite :
V2 (che
è
la velocità finale della massa m2 urtata e ß2 l'
angolo di V2 con l'asse x) .
Ecco le formule finali :
tg ( ß2 ) = V1*sin( ß1
) / [Vo - V1*cos( ß1 )]
V2 = m1*V1*sin(
ß1 ) / [ m2* sin ( ß2 ) ]
Ed ecco i risultati
di un esempio numerico :
Se : m1 = 1 (kg) , Vo = 10 (m/s) , V1 = 6 (m/s) , β1 = 52,9°, m2 = 2 (kg)
Risultati :
V2 = 7,98 (m/s) , β2 = 36,87° , Eo
= 50 (J)
, Efin = 49,8 (J) => Urto quasi elastico

Nessun commento:
Posta un commento