DINAMICA DEI SISTEMI ROTANTI.Un peso cadendo mette in rotazione un verricello (due ruote) e trascina orizzontalmente un'altra massa.

DINAMICA DEI SISTEMI ROTANTI : Caduta verticale di una massa, conseguente rotazione del verricello e trascinamento di una seconda massa.

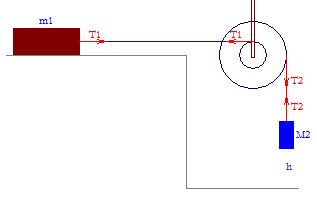
La massa M₂ cadendo di h mette in rotazione le due carrucole (solidali fra loro e di raggi  r₁  ed  R₂)   trascinando la massa m_1.  Attriti  nulli.

Noti  i valori delle masse, dei raggi delle  due ruote solidali, del loro momento d’inerzia e dell’altezza h di caduta di M₂, verranno calcolate le velocità finali (diverse) delle due masse, le loro accelerazioni (diverse), l’accelerazione angolare α (uguale per le due carrucole),  la loro velocità angolare finale e le tensioni dei fili T₁ e T₂ (supposti di massa trascurabile).

ooooo

Nell’ipotesi di puro rotolamento possiamo applicare il Principio di conservazione dell’energia col seguente bilancio energetico :

M_2*g_*h = I_*ω² / 2  +  M_2*V₂² / 2  +  m₁*v₁² / 2

Si può capire facilmente  che la massa M₂, cadendo di h, comunica energia  cinetica a se stessa, ad m₁ ed energia di rotazione alle due carrucole.

Al solito immagineremo di tagliare i due fili (lasciando le quattro forze di tensione (uguali a due a due in modulo, ma di versi opposti).

Essendo queste forze costanti comunicheranno un’accelerazione angolare α costante ed una velocità angolare ω crescente durante la caduta di M₂.

Le  velocità   V₂   e    v₁  sono  date  da  :

V₂ = R_{2 *} ω      e     v₁ = r_{1 *} ω               e se sostituiamo questi valori nell'equazione precedente, potremo calcolare, per prima la velocità angolare  finale ω  e  dopo  le due velocità finali  V₂  e   v₁ delle due masse.

E' facile capire che :

ω² (finale) = 2_*M_2*g_*h / ( I + M_2*R₂² + m_1*r₁² )

ed ecco le altre tre equazioni che dovremo utilizzare :

M_2*g  -  T₂  =  M_{2 *} a₂ ,

T₁ = m_1*a₁ ,

T_2*R₂ - T_1*r₁ = I _* α  ,

 essendo : α =  a₁ / r₁  =  a₂ / R₂  l’accelerazione angolare delle due ruote solidali, che è ovviamente la stessa_, ma non le accelerazioni delle due masse, che risultano date da :

a1 = M_{2 *} g _* R₂ / (m_{1 *} r₁ + M_{2 *} R₂ ² / r₁ + I / r₁)

a₂ = a_{1 *} R₂ / r₁

Quindi possiamo calcolare le due forze di tensione :

T₁ = m_1*a₁ ,      T₂ =  M_{2 *} g  -  M_{2 *} a_{1 *} R₂ / r₁

Ed ecco i risultati d:el programma in Visual Basic :

Dati :                              
             
   Risultati : ω = 6,67  (rad/s) , v1 = 0,67  (m/s) , V2 =  2,67  (m/s)
                        a₁ = 0,18  (m/s²) ,  a₂ =0,71 (m/s²) , α = 1,8  (rad/s²)
                        T1 = 3,56 (N) ,    T2 = 45,44 (N)

oooooo