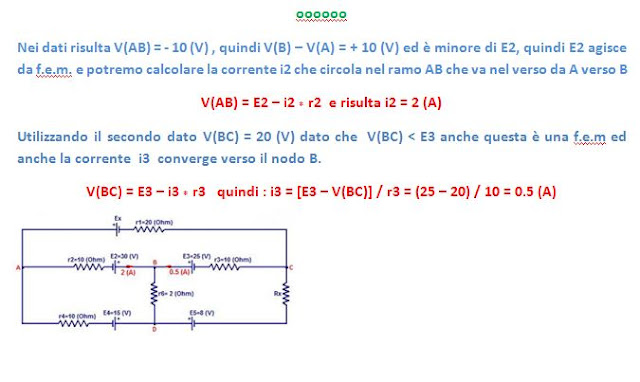
Consideriamo una maglia
(cioè un circuito chiuso), contenente più generatori. Questa ne contiene
tre (E1, E2, E3).
Come calcolare la corrente ed il verso in
cui circola ?
Innanzitutto osserviamo che due (E1
ed E2) dei tre generatori, tendono a mandare la corrente in verso orario, mentre il terzo tende a
mandarla in verso antiorario.
S'intuisce facilmente che
prevale il generatore E3 e che la
corrente circolerà in verso antiorario e che
l'intensità di questa corrente abbia il valore :
i = (E3-E1-E2)/(r1+r2+r3+r4)
= 0.25 (A).
Comunque, per dimostrare questo risultato,
seguiremo un procedimento più lungo, allo scopo di
dimostrare il 2° principio di Kirchhoff anche nel caso di un circuito
costituito da due o più maglie.
Ci
baseremo sull'identità : [V(A)-V(B)]+[V(B)-V(C)] + [V(C)-V(D)] +
[V(D)-V(A)]= 0
Fissiamo arbitrariamente come verso positivo di questa corrente, quello ' orario ', anche se
abbiamo intuito che la corrente circolerà nel verso opposto.
Cominciamo col calcolare la prima
delle quattro d.d.p : V(A) -V(B) = + i * r4
(positiva perché la corrente, convenzionalmente è costituita dal movimento di
cariche positive che si spostano dai punti a potenziale maggiore
verso punti a potenziale minore.
V(B)-V(C) = [V(B)-V(M)] + [V(M)-V(C)]
= i * r2 - E2.
La d.d.p. V(M)
-V(C) è negativa perché, muovendoci nel verso positivo
scelto, (quello orario), incontriamo per primo il morsetto negativo di E2.
Analogamente risulterà : V(C) -
V(D) = + E3 + i * r3 ,
V(D)-V(A) = i * r1
- E1. Sostituendo nella
(1), si ha : i * r4 + i * r2
- E2 + E3 + i * r3
+ i * r1 - E1 = 0 , da cui risulta
i = (E1+E2-E3)
/ (r1+r2+r3+r4) = - 0.25 (A).
Il segno negativo
della corrente ci dice che il verso reale è opposto a quello orario ipotizzato.





Nessun commento:
Posta un commento