Esercitarsi a leggere le scale di Amperometri e Voltmetri (prima di usarli in Laboratorio) e capire cos'è la loro 'classe di precisione'.

La corrente indicata dall'indice rosso vale 66 (mA),
l'errore assoluto massimo = (1.5 / 100) * 100 (mA) = 1.5 (mA) , arrotondato a 2 (mA).

La corrente indicata dall'indice azzurro vale 180 (mA)
l'errore assoluto massimo = (1.5/100)*300 (mA) = 4.5 (mA), arrotondato a 5 (mA)

Segue un esempio di lettura di una scala Voltometrica :

Per finire riteniamo molto utile un esempio di calcolo dell'errore assoluto massimo sulla misura di una resistenza elettrica :

A questo punto gli allievi sono pronti per andare in Laboratorio di Fisica per La Verifica sperimentale della legge di Ohm.

oooo

Esercitiamoci con circuiti contenenti fem e fcem per dimostrare il 2° Principio di Kirchhoff.

  Esercitiamoci con circuiti elettrici con f.e.m. ed f.c.e.m. e dimostriamo il 2° Principio di Kirchhoff.

Consideriamo  una  maglia (cioè  un circuito chiuso), contenente più generatori. Questa ne contiene tre (E₁, E₂, E₃). 

Come calcolare la corrente ed il verso in cui circola ?

Innanzitutto osserviamo che due (E1 ed E2)  dei  tre  generatori, tendono a mandare la corrente in verso orario,  mentre  il  terzo tende a mandarla  in verso antiorario.

 S'intuisce facilmente che  prevale il  generatore  E₃  e  che  la corrente  circolerà  in  verso  antiorario e che  l'intensità di questa corrente abbia il valore :

 i = (E₃-E₁-E₂)/(r₁+r₂+r₃+r₄) =  0.25 (A).

Comunque, per  dimostrare  questo  risultato, seguiremo  un  procedimento più lungo, allo  scopo  di dimostrare il 2° principio di Kirchhoff anche nel caso di un circuito costituito  da due o più maglie.

Ci baseremo sull'identità :  [V(A)-V(B)]+[V(B)-V(C)] + [V(C)-V(D)] + [V(D)-V(A)]= 0

 Fissiamo  arbitrariamente  come  verso  positivo  di  questa  corrente, quello ' orario ', anche se abbiamo intuito che la corrente circolerà nel verso opposto.

Cominciamo  col calcolare la prima delle quattro  d.d.p :  V(A) -V(B) = + i _* r₄  (positiva perché la corrente, convenzionalmente è costituita dal movimento di cariche positive che si spostano dai punti  a  potenziale maggiore verso punti a potenziale minore.

 V(B)-V(C) = [V(B)-V(M)] + [V(M)-V(C)] =  i _* r₂  -  E₂.

  La  d.d.p. V(M) -V(C)  è negativa  perché,  muovendoci nel verso positivo scelto, (quello orario), incontriamo per primo il morsetto negativo di E₂.

 Analogamente risulterà :  V(C) - V(D) = + E₃  +  i _* r₃ ,       V(D)-V(A)  =  i _* r₁  -  E₁.  Sostituendo  nella  (1),  si  ha : i _* r4  +  i _* r₂  -  E₂  + E₃  +  i _* r₃  +  i _* r₁ - E₁ = 0 , da cui risulta 

 i = (E₁+E₂-E₃) / (r₁+r₂+r3+r4) = - 0.25 (A).

 Il segno negativo della corrente ci dice che il verso reale è opposto a quello orario ipotizzato.

oooooo

OTTICA : Indice di rifrazione assoluto e relativo.

oooooooo

Una massa oscilla trasversalmente di moto armonico fra due elastici.

UNA MASSA OSCILLA TRASVERSALMENTE FRA DUE ELASTICI.

 

                                     Una massa m, centrata fra due elastici, viene spostata di un piccolo tratto y in direzione trasversale e abbandonata ad oscillare.

 Vogliamo dimostrare che sulla massa agisce una forza di richiamo proporzionale allo spostamento y,  per cui il suo moto sarà armonico.

Le due componenti orizzontali  T_x delle tensioni, si annullano,  mentre  le  due T_y si sommano e danno  F_y=2_*T_*sin (ß).

 Ma se lo spostamento y è piccolo, sarà  sin (ß) = tg (ß) = y / L.  Quindi risulta :

 F_y = - 2 _* T _* y  /  L  =  - k _* y   (k=2*T/L e avendo orientato l'asse  y  verso l'alto). 

Quindi ' F_y '  è  una forza di richiamo di tipo elastico e la massa ' m ' oscillerà  di  moto armonico,  con  pulsazione  :    

Se ad es. m = 0.005 (kg) , L = 0.4  (m) , T = 100  (N) , risulta una frequenza di 50.3  (Hz)

ooooo

STUDIO SPERIMENTALE DELLA TRAIETTORIA PARABOLICA DI UNA PALLINA LANCIATA CON VELOCITA’ INIZIALE ORIZZONTALE.

STUDIO SPERIMENTALE DELLA TRAIETTORIA PARABOLICA DI UNA PALLINA LANCIATA CON VELOCITA’ INIZIALE ORIZZONTALE

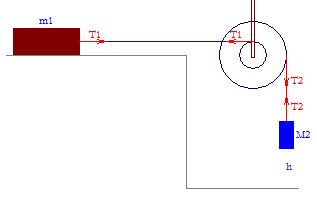
 Una  sferetta  partirà  con  velocità  iniziale  nulla,  dalla  cima  di  una  rampa  curva  (alta   una  decina  di centimetri), quindi proseguirà la sua corsa sul piano orizzontale (a velocità Vo quasi costante, se gli attriti sono stati ridotti al minimo). Infine volerà verso il pavimento sottostante (cadendo per un'altezza h .. misurata).

Applicando le leggi della Fisica, imparate  fino questo momento e immaginando di conoscere Vo ed  h,  calcoleremo il valore della gittata, cioè la distanza sul pavimento alla .... fine del suo volo.

 Dopo  aver  fatto  il  calcolo teorico della gittata, metteremo  un  barattolo nel punto previsto. Se  la  sferetta  ci  cadrà dentro .. potremo affermare  che  le leggi della  Fisica  che  abbiamo utilizzato fino a questo momento sono ... valide.

Per far capire che il tempo di volo dipende solo dall’altezza della caduta ma non dalla velocità orizzontale, faremo partire due sferette nello stesso istante da una data altezza. La prima verrà abbandonata con velocità iniziale nulla,  mentre  la  seconda sarà lanciata orizzontalmente verso destra. 

Provando con due monete,  si dovrebbe udire il contatto col pavimento nello stesso istante.  Sapete già che in una caduta in verticale (senza velocità iniziale verticale) h = g*t ^2 / 2, quindi 

qualunque sia la velocità orizzontale all’ inizio del salto verso il basso.

Dopo la scivolata nel tratto curvo della rampa, la sferetta percorre il tratto rettilineo sul quale posizioniamo due fotocellule per poter cronometrare il tempo di passaggio della sferetta. Gli attriti sono ridotti al minimo, per cui la velocità si mantiene costante e ripetiamo la misura almeno tre volte per determinare un valore medio del tempo e quindi della velocità Vo con la quale alla fine salterà verso il pavimento.

Una volta misurato V_o, come prevedere il valore della gittata? Abbiamo già calcolato il tempo di volo, la resistenza dell’aria sulla sferetta d’acciaio è veramente minima, data anche la bassa velocità, quindi la gittata orizzontale avrà il valore : 

xG =  gittata  = V_{o *}  t_(volo) .

Siamo pronti.

Posizioniamo un bicchierino di plastica sul pavimento dove dovrebbe cadere la sferetta. Possiamo anche staccare il tratto rettilineo della guida (ma non è indispensabile). 

Ricordo ancora l’urlo di gioia degli alunni. Tutti gli anni infallibilmente si faceva canestro. La loro gioia in quei momenti forse non era inferiore a quella di una partita ai mondiali di calcio, quando l’Italia vinceva.

Le leggi della Fisica, studiate fino ad ora si sono sempre rivelate valide. Aveva ragione Galileo quando disse che LA NATURA E’ SCRITTA COL LINGUAGGIO DEI NUMERI. E’ davvero incredibile, spesso anche per lo stesso insegnante..

oooooo

BREVE TEORIA PER L’ESERCITAZIONE DI LABORATORIO

Una sferetta è lanciata dal punto  O  con  velocità  iniziale Vo  orizzontale. Il suo moto risulta composto  da  un componente orizzontale uniforme, dato  che  in questa direzione non ci sono forze e da un componente verticale, uniformemente accelerato.

Nella direzione verticale a= g =  9.8  (m/s ²),  essendo g  l’accelerazione di gravità.

L'ascissa e l'ordinata (x,y)  di un punto generico saranno quindi date da  :

                                  x  =  V_o *  t       ;      y  =  g _* t ²  /  2

Se si ricava il tempo   t  = x  / V_o  dalla prima e lo sostituiamo nella seconda,  otteniamo  l'equazione della traiettoria (che è un arco di parabola)     :

(1)          y  =  g _* x ²  / (2 _* V_o ²)

In  ogni  punto  della traiettoria parabolica, la componente orizzontale della velocità mantiene il valore V_o costante, mentre la componente verticale  V_y = g _* t  aumenta in proporzione al tempo. La somma vettoriale di V_o e V_y fornisce la velocità totale del corpo nell'istante  t .  

E’  la  componente verticale V_y  che sommandosi vettorialmente con la componente orizzontale V_o provoca un’ inclinazione crescente verso il basso della velocità totale della sferetta, che deve risultare  tangente alla traiettoria parabolica in ogni punto.

V ²  =   V_o²  +   V_y²   =    V_o²  +  (g _* t)²

h è l'altezza del tavolo da cui cade la sferetta nel suo volo verso il pavimento.

gittata = x_(max) =  V_o  *  t _(volo)

Il rapporto V_y / V = cos (α)  fornisce  il  valore  del  coseno  dell’angolo d’inclinazione, rispetto alla verticale, della velocità totale V in ogni istante del volo.

ooooo

Una massa collegata a due molle, oscilla di moto armonico.

oooo

Un'equazione differenziale utilissima in Fisica per lo studio della corrente elettrica nella fase transitoria di chiusura di un circuito con induttanza e resistenza.

oooooo

Studio del transitorio induttivo con circuito contenente tre resistenze (utilizzando il Principio di Thevenin).

oooooooooo

Carica di un condensatore in un circuito che richiede l'uso del Principio di Thevenin.

Calcolo della corrente di carica nel condensatore C

Supponiamo che si vogliano  calcolare le tre correnti I₁, I₂ e I₃ durante il regime transitorio, quindi in istanti successivi all’istante t=0 della chiusura del tasto ‘ t ‘.

Supponiamo che siano dati i valori seguenti :

V_o=12 (V), R₁ = 40 (Ω), R₂ = 60 (Ω), R₃ = 6 (Ω) , C = 2 (µF)

Per calcolare la corrente i₃ , come diremo dopo, basterà utilizzare il secondo circuito con i valori V_th  ed  R_th che non sono altro che la f.e.m. equivalente e la resistenza equivalente del Principio di Thevenin (da rivedere se non si ricorda) applicato fra le armature del primo circuito.

Per il calcolo della resistenza equivalente R_th basta immaginare di togliere il condensatore, cortocircuitare V_o (lasciando tutte le resistenze) e con un Ohmetro misurare la resistenza (o calcolarne il valore) fra i punti in cui c’era il condensatore.

Non dovrebbe essere difficile capire che   
R_th = R_1*R₂/(R₁+R₂) + R₃ = 24 + 6 = 30 (Ω)   dato che per l’ohmetro R₁ ed R₂ sono in parallelo fra loro e in serie con R₃.

V_th è la d.d.p. che ci sarebbe fra le armature del condensatore (senza il condensatore), quindi fra i punti M ed N del circuito (senza il condensatore, ma con tutto il resto del primo circuito). 

In questo circuito non c'è corrente nella resistenza R₃, quindi :

V_th = V_M – V_N = [ V_o / (R₁+R₂) ]_*R₂ = (12 / 100)_*60 = 7.2 (V)

Quindi ecco i valori della corrente I₃ del primo circuito :

I₃ = (V_th/R_th) _* e ^–t/Rth*C

Se ad es.  t = 0.0001 (s) risulta :    I₃ = 0.2032 (A)

Volendo calcolare le correnti negli altri rami nello stesso istante utilizzeremo le equazioni seguenti (nel primo circuito) :

I₁ = I₂+I₃

-V_o +I_1*R₁ + I_2*R₂ = 0  (nella maglia inferiore)

Due equazioni e due incognite, quindi possiamo calcolare le correnti : I₂=0.039 (A), I₁=0.24 (A)

A regime il condensatore rimane carico alla d.d.p. di 7.2 (V) ,   I₃ = 0  e  Q = 14.4 (µC),      (potrebbe essere staccato). 

Nella maglia inferiore circolerà una stessa corrente pari a :  I = V_o / (R₁+R₂) = 0.12 (A).

Nel condensatore avviene qualcosa di simile di ciò che succede ad una fila di persone appena aprono il negozio in cui ci soni i famosi saldi. All’apertura la corrente è grandissima, ma le persone arrivate per prime frenano le altre, spesso anche per egoismo. In realtà  sono le cariche già arrivate sulle armature che respingono le successive, frenandone gli .. ardori.

oooooo

IL PRINCIPIO DI THEVENIN (molto importante per Elettrotecnica ed Elettronica).

ooooooo

DINAMICA DEI SISTEMI ROTANTI.Un peso cadendo mette in rotazione un verricello (due ruote) e trascina orizzontalmente un'altra massa.

DINAMICA DEI SISTEMI ROTANTI : Caduta verticale di una massa, conseguente rotazione del verricello e trascinamento di una seconda massa.

La massa M₂ cadendo di h mette in rotazione le due carrucole (solidali fra loro e di raggi  r₁  ed  R₂)   trascinando la massa m_1.  Attriti  nulli.

Noti  i valori delle masse, dei raggi delle  due ruote solidali, del loro momento d’inerzia e dell’altezza h di caduta di M₂, verranno calcolate le velocità finali (diverse) delle due masse, le loro accelerazioni (diverse), l’accelerazione angolare α (uguale per le due carrucole),  la loro velocità angolare finale e le tensioni dei fili T₁ e T₂ (supposti di massa trascurabile).

ooooo

Nell’ipotesi di puro rotolamento possiamo applicare il Principio di conservazione dell’energia col seguente bilancio energetico :

M_2*g_*h = I_*ω² / 2  +  M_2*V₂² / 2  +  m₁*v₁² / 2

Si può capire facilmente  che la massa M₂, cadendo di h, comunica energia  cinetica a se stessa, ad m₁ ed energia di rotazione alle due carrucole.

Al solito immagineremo di tagliare i due fili (lasciando le quattro forze di tensione (uguali a due a due in modulo, ma di versi opposti).

Essendo queste forze costanti comunicheranno un’accelerazione angolare α costante ed una velocità angolare ω crescente durante la caduta di M₂.

Le  velocità   V₂   e    v₁  sono  date  da  :

V₂ = R_{2 *} ω      e     v₁ = r_{1 *} ω               e se sostituiamo questi valori nell'equazione precedente, potremo calcolare, per prima la velocità angolare  finale ω  e  dopo  le due velocità finali  V₂  e   v₁ delle due masse.

E' facile capire che :

ω² (finale) = 2_*M_2*g_*h / ( I + M_2*R₂² + m_1*r₁² )

ed ecco le altre tre equazioni che dovremo utilizzare :

M_2*g  -  T₂  =  M_{2 *} a₂ ,

T₁ = m_1*a₁ ,

T_2*R₂ - T_1*r₁ = I _* α  ,

 essendo : α =  a₁ / r₁  =  a₂ / R₂  l’accelerazione angolare delle due ruote solidali, che è ovviamente la stessa_, ma non le accelerazioni delle due masse, che risultano date da :

a1 = M_{2 *} g _* R₂ / (m_{1 *} r₁ + M_{2 *} R₂ ² / r₁ + I / r₁)

a₂ = a_{1 *} R₂ / r₁

Quindi possiamo calcolare le due forze di tensione :

T₁ = m_1*a₁ ,      T₂ =  M_{2 *} g  -  M_{2 *} a_{1 *} R₂ / r₁

Ed ecco i risultati d:el programma in Visual Basic :

Dati :                              
             
   Risultati : ω = 6,67  (rad/s) , v1 = 0,67  (m/s) , V2 =  2,67  (m/s)
                        a₁ = 0,18  (m/s²) ,  a₂ =0,71 (m/s²) , α = 1,8  (rad/s²)
                        T1 = 3,56 (N) ,    T2 = 45,44 (N)

oooooo

Studio teorico della gittata da una data altezza con velocità iniziale inclinata sull'orizzonte.

oooo

EQUAZIONI PARAMETRICHE DI UN MOTO PARABOLICO.

ooooooo

Equazioni parametriche di un moto rettilineo uniforme.

oooooooo

Energia di rotazione di due masse fissate su manubrio rotante, al variare della posizione dell'asse di rotazione.

Calcolo dell' Energia di rotazione di due masse fissate su manubrio rotante, al variare della posizione dell'asse di rotazione.

oooooooo

DINAMICA DEI SISTEMI RIGIDI ROTANTI : Un verricello solleva una massa di una data altezza.

 Un forza F applicata ad un Verricello solleva una massa ad una data altezza

Se sono noti i raggi r1 ed R2 delle  due  ruote solidali, il loro momento  d’inerzia I, la forza F, la massa m e l'altezza h del sollevamento,  verrà calcolata l'accelerazione di m, la tensione T del filo, lo  spostamento s della forza F, il suo lavoro e la potenza media W.

Al solito fingiamo di tagliare il filo lasciandoci le due tensioni T, quindi :

F _* R₂  -  T _* r₁  =  I _* α   ,     (essendo α  = dω / dt     l'accelerazione angolare)

T - m _* g = m _* a  ,  ed     a = r_{1 *} α  (verso l'alto)

Dalle  tre equazioni precedenti si è ricavato il valore dell’accelerazione verso l’alto della massa m :

a = (F _* R₂ - m _* g _* r₁) / (m _* r₁ + I / r₁)

Il sollevamento della massa  m  dell'altezza h provoca una rotazione di un angolo  h / r1 (radianti), mentre la forza F si sposta orizzontalmente di un tratto  s  tale che : 

s / R₂ = h / r₁ , 

quindi si può calcolare il suo lavoro : L =  F _* s .

Il moto è uniformemente accelerato con velocità iniziale nulla, quindi : h = a _* t_s²/ 2,  e si ricava il tempo della salita 

La velocità  non  è  costante  durante la salita  per cui  la  potenza media : W = F _* s / t_s

Ed ecco dei risultati ottenuti con il mio programma .Exe in Visual Basic

Risultati : a = 1.7  (m/s²) , s = h_*R₂/r₁ = 10 (m) , L = F_*s = 4000 (J) , T = m_*(g+a) = 460  (N) ,
 t_s =2.43  (s) , W = L / t_s = 1649  (W)

Il momento delle forze esterne  M^(e) = F_*R₂ - T_*r₁ agenti sul Verricello è costante per cui risultano costanti sia l’accelerazione angolare  ‘ α ‘ che quella lineare ‘ a ‘.

oooooo