UTILIZZIAMO VELOCEMENTE UN MILLI O MICROAMPEROMETRO COME OHMETRO

L'Ohmetro è uno strumento che consente di fare una misura rapidissima, (anche se  non troppo precisa), della resistenza elettrica di un conduttore.

Permette di  verificare l'assenza di interruzioni in un tratto di un circuito  o  la  presenza  di  un  cortocircuito, per  cui questo strumento è veramente prezioso per  il  controllo  di apparecchiature elettriche ed elettroniche.

Il principio su cui si basa l'ohmetro è  molto semplice.

Più grande è la R_x inserita fra i due puntali (P₁ e P₂), più pic-cola  è la corrente misurata dal milli o micro amperometro A.

 Con  R_x=0 , quindi mettendo in  contatto  (o come  si  suole dire 'in cortocircuito' fra loro)  i due puntali  P₁  e   P₂ ,  si regola la corrente (misurata da 'A'), al fondo scala.

 Senza  più  spostare il cursore  del reostato, si inseriranno (sempre fra  P₁ e P₂), in successione, una serie di resistenze campioni (quindi di valore conosciuto)  e si prenderà nota dei valori corrispondenti delle correnti (o solo delle ' divisioni ').

Con questi valori, si potrà costruire il cosidetto 'diagramma di taratura' dell'ohmetro, con i valori delle correnti (o delle divisioni) in ordinata e quelli delle resistenze campioni corrispondenti, in ascissa.

Disegnato il grafico, in base al numero di divisioni indicate da A, con una resistenza incognita  R_x, si potrà dedurne il valore. (Un'esperienza analoga si fa in 'meccanica' per tarare una molla).

La  pila  dev'essere  sempre  abbastanza  carica, da poter mandare (con R = 0)  in  fondo scala l'amperometro ' A ', diversamente va sostituita.

Rp è una resistenza di protezione dell'amperometro A.

00000000000000000

UTILIZZIAMO L'OMETRO PER UNA VERIFICA SPERIMENTALE DI RESISTENZA TEORICA

ooooooo

Esercitarsi alla lettura di amperometri e voltmetri prima di usarli nel Laboratorio di Fisica

LETTURA DI UNA DIFFERENZA DI POTENZIALE CON UN VOLTMETRO

Il circuito elettrico di base

Ricordo che tutti gli anni lanciavo una sfida ai miei alunni e chiedevo se ci fosse qualcuno di loro disposto a montare questo circuito con gli occhi bendati e iniziava la lotta perché tutti se la sentivano di collegare i 7 fili conduttori. La prova era sempre un successo e così acquistavano la sicurezza necessaria per eseguire le misure MA CON GLI OCCHI NON PIU' BENDATI MA BEN APERTI  per non bruciare strumenti ... costosi.

ooooooo

La matematica che serve per la fisica

  LA MATEMATICA CHE SERVE PER LA FISICA

EQUAZIONI DI PRIMO E DI SECONDO GRADO (NECESSARIE)

UNA CURVA MOLTO IMPORTANTE : LA PARABOLA

°°°°°°°°°°°°°°

RISOLUZIONE GRAFICA DI UN'EQUAZIONE DI SECONDO GRADO

°°°°°°°°°

INTERSEZIONI  FRA  UNA  FAMIGLIA  DI  RETTE  E  UNA  PARABOLA

°°°°°°°°°°°°°°°°°

LE DISEQUAZIONI TRIGONOMETRICHE DI BASE

Ed ecco il caso : sin (x) > a

Segue il caso : cos (x) < a

Per finire ecco il caso : cos (x) > a

oooooooooooo

LA FUNZIONE ESPONENZIALE

oooooooo

COS'E' IL  LOGARITMO  DI  UN  NUMERO ?

°°°°°°°°°°°°°°°°

GLI ASINTOTI DELLE FUNZIONI

ooooooooooo

LIMITI DI UNA FUNZIONE (RESI  COMPRENSIBILI)

ooooooooo

FINE

La fisica di base con un click da 13 a 25 anni

Su AMAZON ci sono  miei libri di Fisica con collegamenti ipertestuali che consentono di visualizzare l'argomento desiderato con un clic del mouse (di circa 200 videate ciascuno).  

VOLUME PRIMO : La Fisica che serve allo studente.DOCX 

VOLUME SECONDO : La Fisica che serve allo studente.DOCX
Imparare l'elettricità partendo dal laboratorio.DOCX

In questo blog desidero mostrare alcune pagine provenienti dai miei programmi aggiornati per oltre 25 anni (mentre insegnavo presso l'ITIS di Livorno per 35 anni, più 4 anni presso l'ITIS di Pisa, e dopo, in pensione dal 1994 al 2018.

 (N.B. PREMERE INSIEME I  TASTI  (Ctrl  e  +) PER INGRANDIRE LE VIDEATE) 

All'età di 84 anni, voglio aiutare ancora i giovani studenti e spero di riuscire a far loro amare la Fisica che  ho mostrato con  un linguaggio molto semplice per raggiungere non solo ragazzi di 13-14 anni, ma anche studenti universitari e anche molti giovani docenti che troveranno in questi due volumi di circa 200 videate ciascuno, esercitazioni  di laboratorio, problemi, test e teoria molto sintetica.

Nei due volumi su AMAZON  ci ho messo la Fisica come l’ho insegnata per 35 anni.

Il collegamento ipertestuale consente di visualizzare il programma che si vuole vedere con  un  

semplice clic del mouse. 

Molti problemi saranno utili anche per gli studenti universitari in ingegneria, medicina, biologia,

 ecc. per superare le difficoltà delle prove scritte.

Animazioni e conteggio delle risposte giuste possono aversi solo con i miei programmi  eseguibili (quindi .Exe) che ho scritto in Visual Basic in un continuo lavoro di miglioramenti e aggiunte che ho messo su Cd già da diversi anni (di non facile pubblicazione da parte delle case editrici,  per la facilità di copia del Cd).

Tutti i disegni sono presi appunto dai miei programmi .Exe scritti in Visual Basic.

Questi due programmi su AMAZON consentono di prepararsi rapidamente per un concorso, per rivedere velocemente argomenti non capiti o perché si era assenti a scuola. Dovrebbe risultare molto più utile del libro di testo perché basta un  clic del mouse per passare velocemente da un argomento all’altro.

Nel 1990, la casa editrice S.E.I di Torino  pubblicò due miei volumi dal titolo  Fisica col  computer (allora scritti   in Turbo Pascal).

°°°°°°°°°°°°

N.B. QUESTI PROGRAMMI INIZIALI DI QUESTO POST SONO TRATTATI PIU' DIFFUSAMENTE NEGLI ALTRI POST SUCCESSIVI DI QUESTO BLOG  (Per cui si possono anche non leggere).

ANALOGIA  IDRICA  CON LA LEGGE DI OHM

Se si apre il rubinetto che mette in comunicazione due recipienti, il liquido si mette in movimento, finché c'è un dislivello.

Per ottenere una corrente di intensità costante è necessario mantenere un dislivello costante, (ad es. con  un rubinetto che immette liquido da una parte ed un foro dall'altra).

Analogamente, per avere  una  corrente elettrica  di  intensità costante in un conduttore, basterà mantenere una  d.d.p. costante ai suoi estremi.

Una pila, un accumulatore, o un alimentatore, sono capaci di  mantenere una  d.d.p. costante  ai   capi di un conduttore e quindi di mantenervi una corrente di intensità costante.

Per ora non è necessario sapere come funziona un generatore elettrico  e   basterà  ricordare  che nel polo positivo esso mantiene un difetto di elettroni e nel negativo, un eccesso.

Se fra questi due poli colleghiamo gli estremi di un conduttore, gli elettroni di conduzione di questo si metteranno in  moto perché attratti dal polo positivo e respinti dal negativo.

Convenzionalmente si dice però che la corrente elettrica è costituita dal movimento di cariche positive, respinte dal polo positivo e attratte dal negativo, anche se è vero il contrario (perché gli elettroni sono stati scoperti successivamente).

oooooooo

VERIFICA SPERIMENTALE DELLA LEGGE DI OHM

Ecco il circuito di base (comune a molte esercitazioni). Prima si fa studiare alla lavagna.

Dal morsetto positivo dell’alimentatore si va col filo conduttore 1 all’estremo di sinistra del reostato, mentre si collega l’altro estremo al polo negativo dell’alimentatore col filo 2.

Con il filo 3 si va dal morsetto di sinistra ‘D‘ del reostato all’ingresso positivo dell’amperometro. 

Dal morsetto negativo dell’amperometro si va col filo 4 all’estremo di sinistra del conduttore R_x e l’altro estremo di R_x viene collegato al cursore del reostato col filo 5 in modo da poter variare la d.d.p ai capi di R_x.

Infine il voltmetro viene collegato con due conduttori (6 e 7) agli estremi di R_x per poter misurare le varie d.d.p. che verranno applicate variando di volta in volta la posizione del cursore del reostato. Per questo circuito sono necessari 7 conduttori con spinotti agli estremi.(Non si fanno saldature).

Ricordo che tutti gli anni lanciavo  la sfida a montare questo circuito con gli occhi bendati e iniziava la lotta perché tutti se la sentivano di provare. Così acquistavano presto la sicurezza necessaria per montare un circuito elettrico (.. dopo, ma con gli occhi sempre ben aperti).

Lo scopo di questa esercitazione è quello di studiare come varia l’intensità della corrente nel conduttore R al variare della d.d.p. V applicata ai suoi estremi.

Prima di chiudere l'interruttore, raccomandavo di assicurarsi che il  cursore  del reostato fosse  più vicino possibile  al 'morsetto doppio D' (per non bruciare i due strumenti di misura).

Per questi raccomandavo di  scegliere  portate  sovrabbondanti, da ridurre successivamente.

Chiuso l'interruttore  ' t '  e  spostato  lentamente il cursore del reostato verso destra,  si può misurare la prima coppia di valori (i, V), facendo  in  modo (se possibile),  che le  indicazioni dei  due strumenti  non cadano al disotto del primo quarto della loro scala, (dove sarebbero meno precise).

Il grafico di vecchie misure (riportato  nella figura accanto), ci consentì di affermare che la d.d.p. V applicata agli estremi del conduttore R  e l'intensità  della  corrente ' i ' che,  di  conseguenza l'attraversa, sono direttamente proporzionali, per cui il loro rapporto : V / i = costante.

E' per l'analogia con le correnti liquide che al valore di questo rapporto si è dato il nome di  'resistenza elettrica'  e  si pone : 

V  /  i  =  R.

In onore di chi scoprì questa legge, la resistenza elettrica si misura in Ohm (il cui simbolo è Ω)

 1 Ω = 1 (V) / 1 (A).

Quindi ha la resistenza di 1 Ω, quel conduttore che, con la d.d.p. di 1 Volt  agli estremi,  viene  attraversato dalla corrente di 1 Ampere.

   1 (Ω ) / 1 (V ) / 1 (A)

PROPAGAZIONE DEGLI ERRORI

°°°°°°

SUBITO DOPO LA VERIFICA SPERIMENTALE DELLA LEGGE DI COMPOSIZIONE DELLE RESISTENZE ELETTRICHE IN SERIE E IN PARALLELO  PASSIAMO AL CALCOLO DELLE CORRENTI CHE PERCORRONO UN CIRCUITO DEL TIPO SEGUENTE.

°°°°°°°°°°°°°

TRASFORMIAMO UN TRIANGOLO DI RESISTENZE ELETTRICHE IN UNA STELLA

Si può verificare sperimentalmente che al triangolo di resistenze R₁,R₂ R₃, si può sostituire una stella, avente per centro un punto ' S ' e  i cui lati sono paralleli alle bisettrici degli angoli del triangolo.

Ciascuna resistenza della stella  si  ottiene  moltiplicando  le resistenze dei due lati del triangolo  (fra i quali è compresa) e dividendo per la somma delle tre resistenze del triangolo (perimetro).

r₁₂ = R_1*R₂ / (R₁+R₂+R₃) ,     r₁₃ = R_1*R₃ / (R₁+R₂+R₃) ,        r₂₃ = R_2*R₃ / (R₁+R₂+R₃)

 Se, per esempio, fosse : R₁ = 20  Ω , R₂ = 50  Ω, R₃ = 30  Ω , risulterebbe :

r₁₂ = 20_*50 / 100 = 10  Ω ,  r₁₃ = 6  Ω , r₂₃ = 15  Ω.

Consideriamo  come primo esempio un circuito molto importante per le applicazioni :

In questo circuito le resistenze non sono collegate né in serie, né in parallelo,  per cui anche se fossero conosciuti i valori delle  6  resistenze e quello di  V_o , non saremmo in grado di calcolare le correnti.

Non sembra esserci alcun triangolo, ma ridisegnando il circuito in maniera leggermente diversa ne vedremo chiaramente uno (dei due presenti).

Nella prossima videata sostituiremo al triangolo di R₁,R₂,R₃ una stella equivalente e potremo rendere calcolabile la resistenza totale e tutte le correnti nelle singole resistenze.

Segue applicazione numerica

Ecco un esempio numerico di questo importante circuito.

Dati : R₁ = 20  Ω , R₂ = 30  Ω , R₃ = 50  Ω , R₄ = 20  Ω   , R₅ = 5  Ω , r = 2  Ω     , V_o = 60  V

   

                                                                                  Calcoli : r₁₂ = 6 Ω , r₁₃ = 10 Ω ,  r₂₃ = 15  Ω

Utilizzando la trasformazione triangolo-stella il

circuito diventa facilmente semplificabile.

Perché r₁₃ risulta in serie con R_{4 ,} quindi :

                       R(SBD) = 30 Ω,

r₂₃  è in serie con R₅  (quindi : R(SCD) = 20  Ω),

Il parallelo R(SD) = 12 Ω è in serie con r₁₂ , quindi

R(AD) = 18 Ω,

R_(tot) = 20  Ω , i_(tot) = 3  A , V(AS) = 18  V , V(SD) = 36  V

Volendo calcolare le correnti nelle resistenze del circuito di partenza, (in R4 ed R5 le abbiamo

calcolate nel secondo circuito, i₄ = 1.2 A ed i₅ = 1.8 A), ci servono le 3 differenze di potenziale :

[ V(AB), V(AC), V(BC)] che possiamo calcolare ancora nel secondo circuito.

Infatti : V(AB) = V(AS) + V(SB) = 18 + 12 = 30 V quindi nel primo circuito : i₁ = i(AB) = 1.5 A

              V(AC) = V(AS) + V(SC) = 18 + 27 = 45 V quindi nel primo circuito : i₂ = i (AC)= 1.5 A

              V(BC) = V(BS) + V(SC) = - 12 + 27 = 15 Vquindi nel primo circuito : i₃= i(BC) = 0.3 A

La resistenza R₃ nel ramo BC è l’unica nella quale la corrente i₃ può avere due possibili versi.

Se V(BC) > 0 la i₃ andrà da B verso C (come nel nostro esempio), se invece V(BC) < 0 la cor-

rente i₃ andrà nel verso da C a B.

Sarà anche possibile il caso in cui V(BC) = 0 per cui risulterà i₃ = 0 (questo caso viene utilizza-

to nel famoso Ponte di Wheatstone, che studieremo.

°°°°°°°°°°°°°°°°°

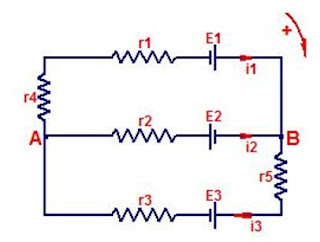
I  PRINCIPI  DI  KIRCHHOFF (DIMOSTRAZIONE)

Consideriamo  una  maglia (cioè  un circuito chiuso), contenente più generatori.

Questa ne contiene tre (E₁, E₂, E₃).

Come calcolare la corrente ed il verso in cui circola ?

Innanzitutto  osserviamo che due (E1 ed E2)  dei  tre  generatori, tendono a mandare la  corrente  in verso  orario,  mentre  il  terzo tende a mandarla  in verso antiorario.

S'intuisce facilmente che  prevale il  generatore  E₃  e  che  la corrente  circolerà  in  verso  antiorario e che  l'intensità di questa corrente sarà :

i = (E₃-E₁-E₂)/(r₁+r₂+r₃+r₄) =  0.25 (A).

Comunque, per  dimostrare  questo  risultato, seguiremo  un  procedimento più lungo, allo  scopo  di dimostrare il 2° principio di Kirchhoff anche nel caso di un circuito costituito da due o più maglie.

Ci baseremo sull'identità :

(1)    [V(A)-V(B)]  +  [V(B)-V(C)]  +  [V(C)-V(D)]  +  [V(D)-V(A)]  =  0.

Fissiamo arbitrariamente come verso positivo  di questa corrente, quello ' orario ', anche se abbiamo intuito che la corrente circolerà nel verso opposto.

Cominciamo  col calcolare la prima delle quattro  d.d.p. :  V(A) -V(B) = + i_*r₄  (positiva perché la corrente, convenzionalmente è costituita  dal  movimento  di  cariche positive che si spostano dai punti  a  potenziale maggiore verso punti a potenziale minore.

V(B)-V(C) = [V(B)-V(M)] + [V(M)-V(C)] = i_*r₂ - E₂.

 La  d.d.p. V(M) -V(C)  è negativa  perché,  muovendoci nel verso positivo scelto, (quello orario), incontriamo per primo il morsetto negativo di E₂.

Analogamente risulterà :  V(C) - V(D) = + E₃  +  i_*r₃ ,       V(D)-V(A)  =  i_*r₁ - E₁.  Sostituendo  nella  (1),  si  ha :

 i_*r4  +  i_*r₂  -  E₂  + E₃  +  i_*r₃  +  i_*r₁ - E₁ = 0 , da cui risulta :

i = (E₁+E₂-E₃) / (r₁+r₂+r3+r4) = - 0.25 (A).

Il segno negativo della corrente ci ricorda che il verso reale è opposto a quello orario ipotizzato.

 oooooooooooooooo

CASO  DI  CIRCUITO  CON  DUE  MAGLIE

Supponiamo di dover calcolare le tre correnti i₁,i₂,i₃ conoscendo le 5 resistenze e le f.e.m. (E₁, E₂, E₃).

Le resistenze r₄ ed r₁ sono in serie fra loro, (come pure r₃ ed r₅) e potrebbero essere sostituite dalle rispettive somme.

Per prima cosa fissiamo a piacere i versi delle tre correnti (i₁, i₂, i₃) incognite ed un verso di percorrenza della singola maglia.

Sapremo solo alla fine se i versi delle correnti sono giusti e invertiremo il verso di quelle che dovessero risultare negative.

Se ci sono tre incognite, ci servono tre equazioni, per poterle calcolare. Dato che la  d.d.p.      V(A) - V(A) = 0 qualunque sia il percorso chiuso che si segue, scegliamo  a  caso una  prima  maglia (ad  es. quella  superiore), per la quale, tenendo conto del fatto che le correnti nei due rami sono diverse tra loro (i₁ ed i₂), scriveremo  :

    (1)   i_1*r₄  +  i_1*r₁  -  E₁  -  E₂  -  i_2*r₂  =  0      e    (2)   i_2*r₂  +  E₂  +  i_3*r₅  +  E₃  +  i_3*r₃ = 0

E' necessario capire che una stessa caduta di tensione (ad es. in r₂)  può avere segno diverso nelle due maglie ed anche una stessa f.e.m. che appartiene a entrambe le maglie.

Se avessimo scelto come verso di percorrenza quello antiorario, avremmo  ottenuto  le  due  stesse equazioni (dato che i segni sarebbero stati tutti opposti).

Manca la terza equazione.  Qualcuno potrebbe pensare di percorrere  la  maglia periferica  (primo e terzo lato), ma si otterrebbe un'equazione  non indipendente (perché combinazione  lineare delle  due  già ottenute). (Anzi, per essere sicuri di scrivere equazioni alle maglie  sicuramente  indipendenti, dopo aver considerato una maglia, bisogna immaginare di .. tagliare uno dei rami fra i due nodi.

La terza equazione necessaria  ce la fornirà il nodo B (o A), per il quale si può scrivere  : 

(3)    i₁ + i₂ = i₃

(principio di conservazione della carica elettrica o Primo Principio di Kirchhoff).

                       oooooooo

TEST SULLA POTENZA ELETTRICA

°°°°°°°°°°°°°

°°°°°°°°°°°°°°°

PREMESSA  AL  CONDENSATORE

Immaginiamo di caricare due dischi metallici, piani  e  paralleli,  di  cui  si  possa  variare  la distanza,  con una  d.d.p. abbastanza  alta di almeno un migliaio di volt).Chiudiamo il tasto  t  per caricare il condensatore C.

Il generatore, per caricare i due dischi (o armature), ha  sottratto  una  certa carica  + Q all'armatura  di destra, che perciò rimane carica negativamente, e l'ha portata su quella di sinistra.

Le due armature,cariche di segno opposto,  si  attirano  e  ci  sembra  lecito aspettarsi che, se le allontaniamo, dopo  aver  riaperto il tasto ' t '   la d.d.p. V, debba aumentare (mentre le cariche rimarranno costanti), dato che il generatore è stato staccato.

Questa previsione  è  basata  sull'analogia (meccanica)  con una molla che viene allungata, per la quale  il  lavoro  fatto produce un aumento della sua energia potenziale (elastica).

L'esperienza conferma le nostre aspettative ed infatti il voltmetro o anche un  comune elettroscopio  rivela un aumento della d.d.p. fra le armature.

 Quindi due lastre conduttrici,  separate da un isolante, che nel nostro caso  è  l'aria,  consentono di accumulare cariche elettriche con una d.d.p. che è tanto minore, quanto minore è la loro distanza.

Se paragoniamo la  d.d.p. al  livello  e  la carica  alla quantità di un liquido contenuto in un recipiente,  comprendiamo che due lastre conduttrici realizzano per le cariche elettriche un insieme di  capacità  tanto maggiore, quanto maggiore è la loro superficie e quanto minore è la loro distanza Un condensatore può essere paragonato ad un ' magazzino di carica ' a dislivello elettrico (d.d.p.)  relativamente basso.

°°°°°°°°°°°°°°°°°°°°°°°°

ANALOGIE FRA CIRCUITI CON RESISTENZE E CIRCUITI CON CONDENSATORI

000000000