DINAMICA DEI SISTEMI : Il pendolo di Maxwell, noto ai bambini col nome di Yo-Yo

UN  GIOCATTOLO MOLTO INTERESSANTE PER LA FISICA : IL PENDOLO DI MAXWELL NOTO COME Yo_Yo

Lo Yo-Yo è costituito da due dischi cilindrici omogenei ciascuno di massa M₁  e  raggio  R₁,  saldati   nella  parte centrale   ad   un manicotto  cilindrico di massa   m₂  e  raggio r₂ << R₁.  Un filo molto sottile  di  diametro trascurabile è avvolto nella parte centrale del manicotto. Se  si  lascia cadere lo Yo-Yo, il filo svolgendosi lo mette in rotazione.

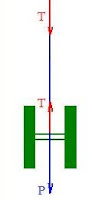
Arrivato in fondo,  per la  sua  inerzia rotazionale  risale  e se ci fosse rotolamen-

to senza strisciamento,  raggiungerebbe  la  posizione  iniziale, e inizierebbe una  serie infinita di corse su e giù, ma gli attriti finiranno per fermarlo.

Vogliamo calcolare la velocità in fondo alla discesa, la velocità angolare massima

 in quel punto, l’accelerazione angolare, quella lineare, il valore della tensione T

del filo ed il tempo impiegato in ogni discesa.

Vogliamo inoltre calcolare il rapporto fra l’energia di traslazione e quella di rotazione.

M _tot  =  2_*M₁ + m₂   ,   P  =  M_tot* g  ,    I  = 2_*M_1*R₁² / 2 +  m_2*r₂² / 2   (I è il  momento d’inerzia)

Il moto è roto-traslatorio e useremo le due equazioni :

T _* r₂  =  I _* α      e       P – T  =   M_{tot *} a                                        (essendo  α l’accelerazione angolare  e

‘ a  ‘ quella lineare, ricordando il legame fra le due   :  a = r_{2 *} α).

Dati :  M₁ = 0.4  (kg)  ,  R₁  =  0.05  (m)  ,   m₂ = 0.2  (kg)  ,  r₂  =  0.01  (m)  ,  h = 1 (m)

Risultati : M_tot = 1.0  (kg)  ,  I  =  0.00101  (kg_*m²)  ,  a  =  0.88 (m/s²)  ,  α  =  88.3  (rad/s²)  ,

                  V (finale) = 1.33  (m/s)  ,  ω (velocità angolare massima) = 133  (rad/s) , t = 1.51 (s)

Energia di rotazione = E_rot = I _* ω² / 2 = 8.92  (J)

Energia di traslazione = E_tr = M_tot*V² / 2 =  0.88  (J)

E_rot + E_tr =  9.8  (J)   ,   E_tr / E_rot  = 9.9 %  ,  Energia potenziale iniziale = M_tot*g _* h = 9.8  (J)

T = 8.92 (N)