Il nonio angolare per apprezzare i primi di grado.

DINAMICA DEI SISTEMI : Il pendolo di Maxwell, noto ai bambini col nome di Yo-Yo

UN  GIOCATTOLO MOLTO INTERESSANTE PER LA FISICA : IL PENDOLO DI MAXWELL NOTO COME Yo_Yo

Lo Yo-Yo è costituito da due dischi cilindrici omogenei ciascuno di massa M₁  e  raggio  R₁,  saldati   nella  parte centrale   ad   un manicotto  cilindrico di massa   m₂  e  raggio r₂ << R₁.  Un filo molto sottile  di  diametro trascurabile è avvolto nella parte centrale del manicotto. Se  si  lascia cadere lo Yo-Yo, il filo svolgendosi lo mette in rotazione.

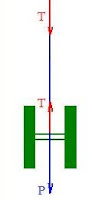
Arrivato in fondo,  per la  sua  inerzia rotazionale  risale  e se ci fosse rotolamen-

to senza strisciamento,  raggiungerebbe  la  posizione  iniziale, e inizierebbe una  serie infinita di corse su e giù, ma gli attriti finiranno per fermarlo.

Vogliamo calcolare la velocità in fondo alla discesa, la velocità angolare massima

 in quel punto, l’accelerazione angolare, quella lineare, il valore della tensione T

del filo ed il tempo impiegato in ogni discesa.

Vogliamo inoltre calcolare il rapporto fra l’energia di traslazione e quella di rotazione.

M _tot  =  2_*M₁ + m₂   ,   P  =  M_tot* g  ,    I  = 2_*M_1*R₁² / 2 +  m_2*r₂² / 2   (I è il  momento d’inerzia)

Il moto è roto-traslatorio e useremo le due equazioni :

T _* r₂  =  I _* α      e       P – T  =   M_{tot *} a                                        (essendo  α l’accelerazione angolare  e

‘ a  ‘ quella lineare, ricordando il legame fra le due   :  a = r_{2 *} α).

Dati :  M₁ = 0.4  (kg)  ,  R₁  =  0.05  (m)  ,   m₂ = 0.2  (kg)  ,  r₂  =  0.01  (m)  ,  h = 1 (m)

Risultati : M_tot = 1.0  (kg)  ,  I  =  0.00101  (kg_*m²)  ,  a  =  0.88 (m/s²)  ,  α  =  88.3  (rad/s²)  ,

                  V (finale) = 1.33  (m/s)  ,  ω (velocità angolare massima) = 133  (rad/s) , t = 1.51 (s)

Energia di rotazione = E_rot = I _* ω² / 2 = 8.92  (J)

Energia di traslazione = E_tr = M_tot*V² / 2 =  0.88  (J)

E_rot + E_tr =  9.8  (J)   ,   E_tr / E_rot  = 9.9 %  ,  Energia potenziale iniziale = M_tot*g _* h = 9.8  (J)

T = 8.92 (N)

Dinamometro con due molle (in serie o in parallelo).

oooooo

Queste videate di miei programmi, che ho scritto in Visual Basic (quindi .Exe), sono di difficile pubblicazione, per la facilità con cui si può copiare un Cd, per cui li ho pubblicati su AMAZON in due volumi, con indice ipertestuale e con un clic del mouse sul Menu si può accedere all'argomento della Fisica che interessa. Studenti dalle medie superiori, fino agli universitari potranno trarne un utilissimo e veloce studio.